Distribusi Uniform kontiniu

Distribusi seragam kontinu adalah distribusi yang peluang setiap peubah acaknya sama.
Fungsi Padat Peluang

dimana a < x < b
a = batas bawah
b = batas atas

Mean
E(X) = (b + a)/2

Varian
Var(X) = (b – a)2/12

Fungsi Pembangkit Momen

Fungsi Karakteristik

Fungsi Pembangkit Peluang
  

 

Distribusi Eksponensial

Distribusi eksponensial diterapkan dalam teori relibilitas (waktu tahan), waktu tunggu, masalah antrian.

Fungsi Padat Peluang

Mean
E(X) = θ-1

Varian
Var(X) = θ-2

Fungsi Pembangkit Momen
Mx(t) = θ (θ – t)-1

Fungsi Karakteristik
Cx(t) = θ (θ – it)-1

Fungsi Pembangkit Peluang
Gx(t) = θ (θ – ln t)-1

Manfaat Minum Air Putih hangat

Orang yang sedang diet biasanya lebih memilih minum air putih hangat karena diyakini lebih cepat menurunkan berat badan dan memiliki banyak manfaat bagi kesehatan. Apa saja manfaatnya? Berikut beberapa manfaat minum air putih hangat : 

1. Pembersihan dan pemurnian, Salah satu manfaat paling penting dari minum air panas adalah efektif dalam membersihkan tubuh. Sistem pencernaan yang buruk dapat dengan mudah diobati dengan minum segelas air panas dua kali sehari, terutama bila diminum di awal pagi. Ini akan membuang racun dari tubuh dan membersihkan sistem tubuh. Anda dapat mencampur air panas dengan madu atau lemon untuk hasil terbaik. 

2. Menyembuhkan sembelit, Ini adalah masalah perut umum yang terjadi karena kurangnya air dalam tubuh, sehingga mengurangi gerakan usus. Minum segelas air hangat saat perut kosong di pagi hari dapat meningkatkan gerakan usus dan menyembuhkan sembelit. Air panas atau hangat dapat memecah partikel makanan dan melewatinya melalui usus. 

3. Menurunkan berat badan, Banyak ahli diet meminta pasiennya untuk minum segelas air panas dengan lemon dan madu setiap hari untuk menurunkan berat badan. Nah, saran ini sangat membantu dalam menurunkan berat badan. Air panas dapat merusak timbunan lemak dari tubuh dan membantu dalam penurunan berat badan. 

4. Obat untuk flu dan batuk, Iritasi pada tenggorokan karena batuk atau tonsil dapat benar-benar menyakitkan. Salah satu manfaat kesehatan dari minum air panas atau hangat, mengurangi nyeri tenggorokan, batuk dan membantu dahak keluar dengan mudah. 

5. Mengeluarkan keringat, Bila minum minuman panas, Anda akan berkeringat banyak. Ketika suhu tubuh naik, tubuh mencoba mendinginkan suhu melalui berkeringat. Berkeringat membantu membersihkan sel-sel kulit dengan mengambil kelebihan air dan garam dari sel dan tubuh. 

6. Meningkatkan aliran darah, Bila Anda minum air panas, timbunan lemak di tubuh dibakar dan timbunan dalam sistem saraf juga diurai. Ini akan meningkatkan sirkulasi darah dalam tubuh dan juga mengeluarkan racun berbahaya. 

7. Mengurangi nyeri, Minum segelas air panas adalah obat rumah yang efektif untuk menyembuhkan kram menstruasi. Jika Anda mengalami sakit perut, sakit kepala atau badan, minum segelas air panas adalah bantuan instan.

PASCAL PERULANGAN

Perulangan adalah sebuah perintah yang menjalankan suatu perintah tertentu berulang-ulang sampai suatu kondisi terpenuhi.disinilah letak kelebihan komputer dibanding manusia, yaitu mampu melakukan hal yang sama berulang kali tanpa kesalahan akibat bosan atau lelah(asalkan script nya bener aja ini,lau script salah berarti komputer mampu membuat kesalahan😀 ).perulangan sering dikenal juga dengan sebutan loop/looping. ada 3 jenis dari perulangan yaitu :


1. perulangan "FOR..DO"
2. perulangan "REPEAT..UNTIL"
3. perulangan "WHILE..DO"

pada perulangan FOR..DO jika di kaitkan kesuatu statement maka akan Ada tiga bentuk perulangan dengan statement for, yaitu:
1. perulangan positif , yaitu perulangan yang perhitungannya dari kecil ke besar. bentuk dari perulangan positif ini adalah “FOR..TO..DO“.
contoh :

program for_do_postiv;
uses wincrt;
var
i : integer;
begin
for i:= 1 to 5 do
writeln('pascal');
readln;
end.

2. perulangan negativ , yaitu perulangan yang perhitungannya dari besar ke kecil. bentuk dari perulangan positif ini adalah “FOR..DOWNTO..DO“.
contoh :

program for_do_negativ;
uses wincrt;
var
i : integer;
begin
for i:= 5 downto 1 do
writeln(i);
readln;
end.

3. perulangan tersarang, suatu perulangan yang didalam nya ada perulangan lainnya. berarti didalam for..do… ada for..do..lagi!
contoh :

program for_do_tersarang;
uses wincrt;
var
i,j : integer;
begin
for i:= 1 to 5 do
begin
for j:= 1 to 5 do
write(j,' ');
writeln;
end;
readln;
end.

setelah membahas tentang for..do…selanjut nya kita akan langsung kepada bentuk perulangan dengan mengunakan repeat..until. pada repeat..until bisa juga mengunakan perulangan yg didalam nya mengunakan perulangan juga.. berikut script/code programnya :

program repeat_until;
uses wincrt;
var
i : integer;
begin
i:= 1;
repeat
i:=i+1;
writeln(i);
until i = 5;
readln;
end.

pada program diatas i sama dengan 1 ketika akan menampilkan i ,maka rumusan dari i+1 dilakukan dan akan berhenti ketika i = 5.

nah selanjut nya tentang while..do…berikut contoh nya :

program while_do;
uses wincrt;
var
i:integer;
begin
i:=2;
while i 3 do
begin
writeln( i );
end;
readln;
end.

pada while..do pada output menghasil bentuk perulangan terus menerus karena i tidak sama dengan 3 maka lakukan cetak 2 terus menerus, ini akan berhenti ketika i sama dengan 3 dan output ketika pendeklarasian i:=3 adalah kosong.
tambahan sedikit :

kalau agan2 binggung coba ketik program pada gambar diatas dan bandingkan.

bonus :
ini hanya bisa dilakukan untuk compiler tertentu

program bonus ;
uses crt;
var i: byte;
begin
for i := 1 to 10 do
begin
textcolor (i) ;writeln('pascal');
end;
readln;
end.

PROGRAM PASCAL FOR DO

A for-do loop is a repetition control structure that allows you to efficiently write a loop that needs to execute a specific number of times.

Syntax

The syntax for the for-do loop in Pascal is as follows −

for < variable-name > := < initial_value > to [down to] < final_value > do 
   S;

Where, the variable-name specifies a variable of ordinal type, called control variable or index variable; initial_value and final_value values are values that the control variable can take; and S is the body of the for-do loop that could be a simple statement or a group of statements.
For example,

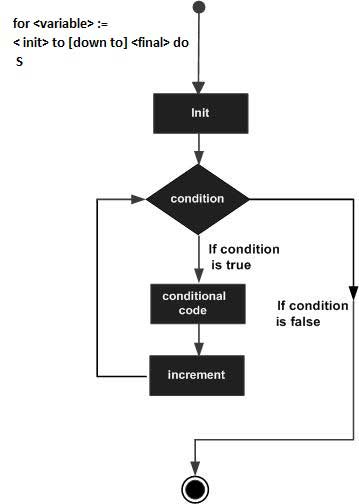
for i:= 1 to 10 do writeln(i);

Here is the flow of control in a for-do loop −

• The initial step is executed first, and only once. This step allows you to declare and initialize any loop control variables.
• Next, the condition is evaluated. If it is true, the body of the loop is executed. If it is false, the body of the loop does not execute and flow of control jumps to the next statement just after the for-do loop.
• After the body of the for-do loop executes, the value of the variable is either increased or decreased.
• The condition is now evaluated again. If it is true, the loop executes and the process repeats itself (body of loop, then increment step, and then again condition). After the condition becomes false, the for-do loop terminates.

Flow Diagram

Example

program forLoop;
var
   a: integer;

begin
   for a := 10  to 20 do
   
   begin
      writeln('value of a: ', a);
   end;
end.

When the above code is compiled and executed, it produces the following result −

value of a: 10
value of a: 11
value of a: 12
value of a: 13
value of a: 14
value of a: 15
value of a: 16
value of a: 17
value of a: 18
value of a: 19
value of a: 20

Statistika

Kuartil, Desil, dan Persentil : STATISTIKA

1. Kuartil
     Kuartil adalah titik yang membagi data yang telah diurutkan menjadi 4 bagian dan masing-masing 25%.
Kuartil ada 3 macam :
a. Kuartil bawah (K1) = 25% dari titik bawah
b. Kuartil tengah (K2) = 50% dari titik bawah 
c. Kuartil atas (K3)     = 75% dari titik bawah

a. Kuartil Data Tunggal

Keterangan :
Ki = kuartil ke-i
i   = ke-i (1, 2, 3)
n  = banyak data

a. Kuartil Data Berkelompok

Keterangan :
Ki = kuartil ke-i
Li = batas bawah kelas kuartil ke-i
Fi = jumlah frekuensi sebelum kelas kuartil ke-i
C  = panjang kelas
n  = jumlah seluruh data
fi  = frekuensi kelas kuartil ke-i
i   = ke-i (1, 2, 3)

2. Desil
     Desil didefinisikan sebagai nilai batas dari sekumpulan data yang telah diurutkan menjadi 10 bagian.

a. Desil Data Tunggal

Keterangan :

Di = desil ke-i

i   = ke-i (1, 2, 3, 4, 5, 6, 7, 8, 9)
n  = banyak data

b. Desi Data Berkelompok

Keterangan : 
Di  = desil ke-i
Li  = batas bawah kelas desil ke-i
i    = 1, 2, 3, 4, 5, 6, 7, 8, 9
Fi  = jumlah frekuensi sebelum kelas desil ke-i
fi   = frekuensi kelas desil ke-i
C  = panjang kelas
n   = jumlah seluruh data

3. Persentil
     Persentil adalah titik yang membagi data yang telah diurutkan menjadi 100 bagian.

a. Persentil Data Tunggal

Keterangan :
Pi = persentik ke-i
i   = 1, 2, 3, 4, 5, .... , 99
n  = banyak data

b. Persentil Data Berkelompok

Keterangan :
Pi = persentik ke-i
Li = batas bawah kelas persentik ke-i
n  = jumlah seluruh data
Fi = jumlah frekuensi sebelum kelas persentil ke-i
fi  = frekuensi kelas persentil ke-i
C = panjang kelas

Contoh :
1. Tentukan kuartil-kuartil dari data: 1, 3, 6, 9, 14, 18, 21

Jawab :
Jumlah data (n) = 7


maka nilai kuartil 1 adalah 3


maka nilai kuartil 2 adalah 9


maka nilai kuartil 3 adalah 18

2. Tentukan kuartil-kuartil dari: 2, 4, 9, 11, 13, 16

Banyak data (n) = 6

1¾ artinya    = data ke-1 + ¾ (data ke-2 - data ke-1)
Jadi nilai K1 = 2 + ¾ (4 - 2)
                K1  = 2 + 1½
                      = 3½


3½ artinya  = data ke-3 + ½ (data ke-4 - data ke-3)
Jadi K2       = 9 + ½ (11 - 9)
             K2   = 9 + 1
                    = 10


5¼ artinya = data ke-5 + ¼ (data ke-6 - data ke-5)
Jadi K3      = 13 + ¼ (16 - 3)
K3               = 13 + ¾
                   = 13¾

3. Perhatikan tabel berikut!

Kuartil ke-1 dari data yang tersaji pada tabel adalah ....
A. 31,13
B. 31,22
C. 31,61
D. 31,63
E. 32,11

Jawab : A
¤ Mencari K1 yaitu :

¤ Kita menggunakan rumus :

Perhatikan tabel di atas !
¹/₄ x 40 = 10
• L1 = 31 - 0,5
        = 30,5
• C  = 26 - 21
        = 5
• F1 = 9
• f1   = 8


¤ Mencari K2 yaitu :

¤ Kita menggunakan rumus :

Perhatikan tabel di atas !
²/₄ x 40 = 20
• L2 = 36 - 0,5
        = 35,5
• C  = 26 - 21
        = 5
• F2 = 17
• f2   = 10


¤ Mencari K3 yaitu :

¤ Kita menggunakan rumus :

Perhatikan tabel di atas !
³/₄ x 40 = 30
• L3 = 41 - 0,5
       = 40,5
• C  = 26 - 21
        = 5
• F3 = 27
• f3   = 6
 

kuarti data tunggal

Kuartil adalah nilai-nilai yang membagi data yang telah diurutkan ke dalam 4 bagian yang sama besar. Dalam menentukan letak kuartil data tunggal, kita harus melihat kondisi jumlah data (n) terlebih dahulu. Kondisi jumlah data (n) tersebut dan penghitungan kuartilnya adalah sebagai berikut.

1. Kuartil untuk jumlah data (n) ganjil dan jika n ditambah 1, hasilnya habis dibagi 4.

2. Kuartil untuk jumlah data (n) ganjil dan jika n ditambah 1, hasilnya tidak habis dibagi 4.

3. Kuartil untuk jumlah data (n) genap dan habis dibagi 4.

4. Kuartil untuk jumlah data (n) genap dan tidak habis dibagi 4.

Rumus-rumus di atas sangat baik digunakan untuk jumlah data banyak. Untuk jumlah data yang kecil, penentuan kuartil lebih mudah ditentukan dengan piramida berikut ini.

1. Kuartil untuk jumlah data (n) ganjil.

2. Kuartil untuk jumlah data (n) genap.

Jika kuartil terletak di antara dua nilai, maka nilai kuartil adalah rata-rata dari kedua nilai tersebut.

Contoh 1:

Berikut ini adalah data panjang jalan di sebuah daerah dalam satuan kilometer.

5, 6, 7, 3, 2

Hitunglah kuartil dari data panjang jalan tersebut?

Jawab:

Karena jumlah data adalah ganjil dan tidak banyak, maka penghitungan kuartil menggunakan piramida kuartil untuk data ganjil.  Pada piramida tersebut, letak kuartil adalah sebagai berikut.

Kuartil 1 terletak antara data pertama dan kedua.

Kuartil 2 adalah data ketiga.

Kuartil 3 terletak antara data keempat dan kelima.

Sebelumnya data diurutkan terlebih dahulu menjadi sebagai berikut.

2, 3, 5, 6, 7

Kuartilnya adalah sebagai berikut

Contoh 2:

Sepuluh orang mahasiswa sebuah perguruan tinggi dijadikan sampel dan dihitung tinggi badannya. Hasil pengukuran tinggi badan kesepuluh mahasiswa tersebut adalah sebagai berikut.

172, 167, 180, 171, 169, 160, 175, 173, 170

Tentukan nilai kuartil dari data tinggi badan mahasiswa tersebut!

Jawab:

Karena jumlah data genap dan tidak banya, maka penentuan kuartil bisa menggunakan piramida kuartil data genap. Pada piramida tersebut, letak kuartil adalah sebagai berikut.

Kuartil 1 adalah data ketiga.

Kuartil 2 terletak antara data kelima dan keenam.

Kuartil 3 adalah data ketujuh.

Sebelumnya, data harus kita urutkan terlebih dahulu. Hasilnya adalah sebagai berikut.

160, 165, 167, 169, 170, 171, 172, 173, 175, 180

Contoh 3:

Jumlah data adalah 223. Tentukan letak kuartilnya!

Jawab

Jumlah data adalah ganjil dan jika n ditambah 1, hasilnya habis dibagi 4. Oleh karena itu penentuan kuartil menggunakan kondisi pertama.

Contoh 4:

Jumlah data adalah 197. Tentukan letak kuartilnya!

Jawab

Jumlah data adalah ganjil dan jika n ditambah 1, hasilnya tidak habis dibagi 4. Oleh karena itu penentuan kuartil menggunakan kondisi kedua.

Contoh 5:

Jumlah data 400. Tentukan letak kuartilnya!

Jawab

Jumlah data adalah genap dan habis dibagi 4. Oleh karena itu penentuan kuartil menggunakan kondisi ketiga.

Contoh 6:

Jumlah data 350. Tentukan letak kuartilnya!

Jawab

Jumlah data adalah genap dan tidak habis dibagi 4. Oleh karena itu penentuan kuartil menggunakan kondisi keempat.