Persamaan Garis Lurus

Persamaan garis lurus adalah suatu garis lurus yang posisinya ditentukan dengan suatu persamaan. Misalnya persamaan  jika kita gambar pada koordinat Cartesius, maka gambarnya akan berbentuk garis lurus.

Cara menggambarnya adalah:

Tentukan titik potong garis tersebut terhadap sumbu , dengan membuat nilai . Pada contoh di atas, maka , sehingga , atau .

Kemudian, tentukan titik potong terhadap sumbu 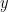, dengan membuat nilai . Pada contoh di atas, maka , sehingga , atau 

Terakhir, hubungkan kedua titik tersebut menjadi sebuah garis lurus. Maka, garis tersebut merupakan garis dengan persamaan .

• Gradien Persamaan Garis Lurus

Gradien adalah besar kemiringan suatu garis terhadap sumbu .

Bentuk umum persamaan garis lurus adalah , dengan m merupakan gradien, sedangkan  suatu konstanta.

Jadi, persamaan yang berbentuk  mempunyai gradien sebesar 2.

Untuk persamaan yang bentuknya , maka gradiennya adalah .

Sedangkan gradien suatu garis yang melalui dua titik  dan , gradiennya didapat dengan menggunakan rumus:

Contoh: Tentukan gradien suatu garis yang melalui titik  dan .

Jawab:

• Hubungan antar gradien pada persamaan garis lurus

Jika suatu garis sejajar dengan sumbu , maka gradiennya adalah 0.

Jika terdapat dua garis yang sejajar, maka gradien kedua garis tersebut sama, atau .

Jika terdapat dua garis yang saling tegak lurus, maka hasil kali kedua gradien tersebut adalah , atau 

Contoh: Garis dengan persamaan  tegak lurus dengan suatu garis yang mempunyai gradien 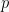. Tentukanlah nilai .

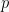Jawaban:

Gradien garis dengan persamaan  adalah .

Karena kedua garis tersebut tegak lurus, maka  atau , sehingga 

Dengan demikian, nilai