METODE TRANSPORTASI APROKSIMASI VOGEL (VAM)
Metode Transportasi adalah suatu metode yang digunakan untuk mengatur distribusi dari sumber – sumber yang menyediakan produk – produk yang sama di tempat- tempat yang membutuhkan secara optimal. Alokasi produk ini harus diatur sedemikian rupa karena terdapat perbedaan biaya transportasi (alokasi) dari suatu sumber ke beberapa tujuan yang berbeda – beda dan dari beberapa sumber ke suatu tujuan juga berbeda – beda.
Ada tiga macam metode dalam metode transportasi:
1. Metode Stepping Stone
2. Metode Modi (Modified Distribution)
3. MetodeVAM (Vogel’s Approximation Method)
Pada sesi ini hanya akan dibahas mengenai metode transportasi dengan metode VAM, sedangkan metodeStepping Stone dan MODI sudah dibahas pada sesi tulisan sebelumnya.
Metode VAM
Teknik pengerjaan pada metode ini berbeda dengan dua metode sebelumnya yaitu metode transportasiStepping Stone dan MODI dimana untuk mendapatkan solusi yang optimal dilakukan berulang-ulang sampai kondisi optimal tersebut terpenuhi. Sedangkan pada metoda VAM ini, sekali kita menentukan alokasi pada satu cell maka alokasi tersebut tidak berubah lagi. Untuk mempermudah penjelasan, kita gunakan contoh yang sama seperti pada metode transportasi sebelumnya.
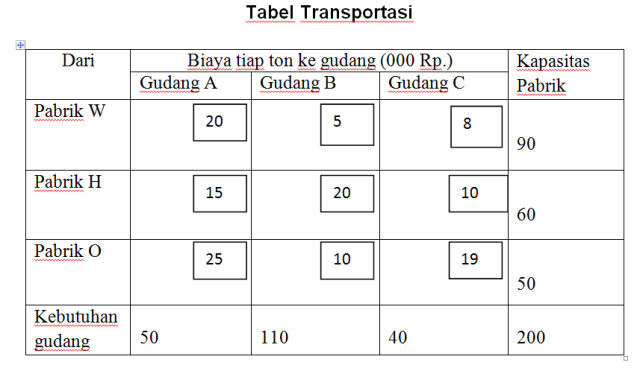
Suatu perusahaan mempunyai pabrik W, H, O dengan kapasitas produksi tiap bulan masing-masing 90 ton, 60 ton, dan 50 ton.; dan mempunyai 3 gudang penjualan di A, B, C dengan kebutuhan tiap bulan masing-masing 50 ton, 110 ton, dan 40 ton. Biaya pengangkutan setiap ton produk dari pabrik W, H, O ke gudang A, B, C adalah sebagai berikut:
Langkah – langkah pengerjaan:
- Susunlah kebutuhan, kapasitas masing-masing sumber dan biaya pengangkutan ke dalam matriks transportasi
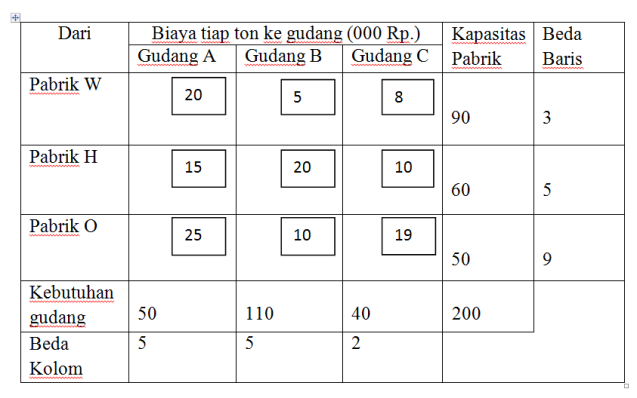
2. Carilah perbedaan dari 2 biaya terkecil, yaitu biaya terkecil dan terkecil ke dua untuk setiap baris dan kolom
3. Pilihlah 1 nilai perbedaan- perbedaan yang terbesar diantara semua nilai perbedaaan pada kolom dan baris. Baris O mempunyai nilai perbedaan terbesar yaitu 9. Bila nilai perbedaan biaya ada 2 yang besarnya sama, maka pilihlah baris atau kolom yang mempunyai biaya terendah.
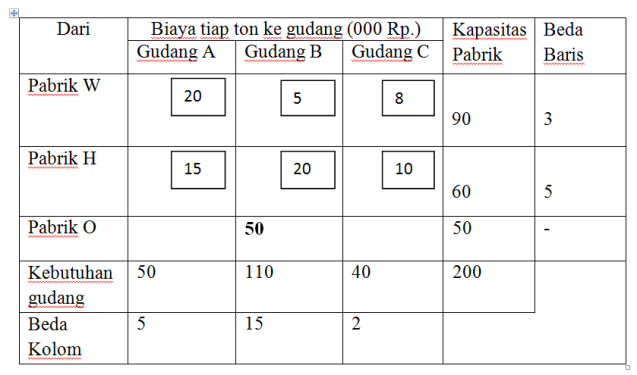
4. Isilah pada salah satu segi empat yang termasuk dalam kolom atau baris terpilih, yaitu pada segi empat yang mempunyai biaya terendah. Isikan sebanyak mungkin yang bisa dilakukan.
5. Karena baris O sudah diisi penuh sesuai dengan kapasitas, maka selanjutnya hilangkan baris O karena baris O sudah tidak mungkin diisi lagi. Kemudian tentukan kembali perbedaan biaya untuk kolom dan baris yang belum terisi. Ulangi langkah-langkah ini sampai semua baris dan kolom sepenuhnya teralokasi.
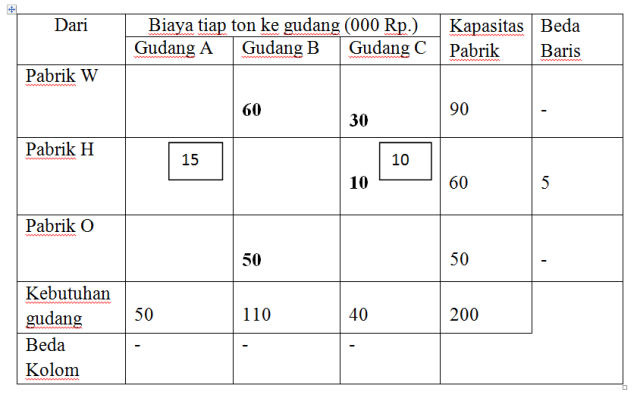
Karena B mempunyai perbedaan terbesar yaitu 15, maka isilah sebanyak mungkin yang bisa diangkut pada kolom B yang mempunyai biaya terendah.
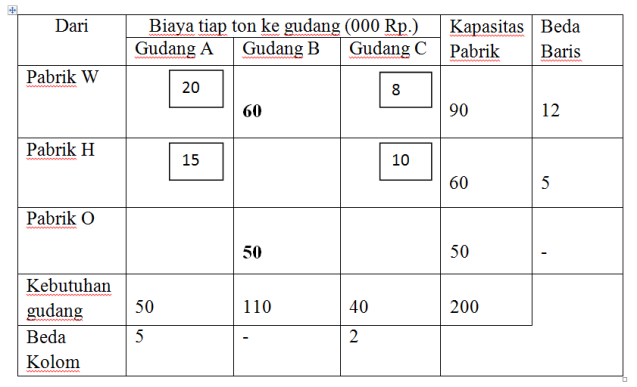
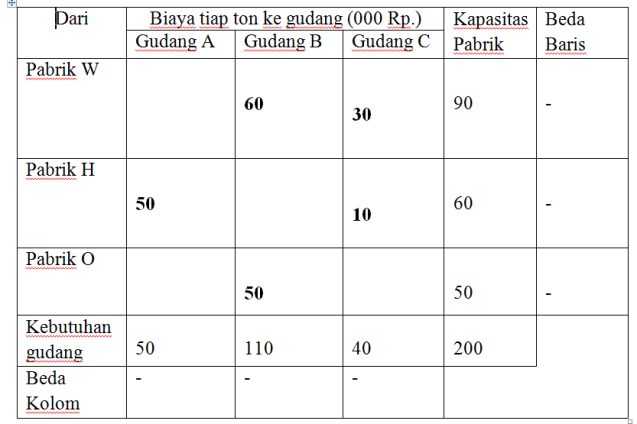
Baris W mempunyai perbedaan terbesar yaitu 12 dan langkah selanjutnya adalah sebagai berikut:
Jadi biaya transportasi yang harus dikeluarkan: 60 (3) +30 (8) + 50 (15) + 10 (10) + 50 (10) = 1890
Tidak ada komentar:
Posting Komentar